|
|
|
|
本日2026年 3月 6日は 旧暦 2026年1月 18日 【赤口】 現在の月齢:16.84
1

先勝 | 月
2

友引 | 火
3

先負 | 水
4

仏滅 | 木
5

大安 | 金
6

赤口 | 土
7

先勝 | 日
8

友引 | 月
9

先負 | 火
10

仏滅 | 水
11

大安 | 木
12

赤口 | 金
13

先勝 | 土
14

友引 | 日
15

先負 | 月
16

仏滅 | 火
17

大安 | 水
18

赤口 | 木
19

友引 | 金
20

先負 | 土
21

仏滅 | 日
22

大安 | 月
23

赤口 | 火
24

先勝 | 水
25

友引 | 木
26

先負 | 金
27

仏滅 | 土
28

大安 | 日
29

赤口 | 月
30

先勝 | 火
31

友引 |
3月 の大安は 5日 11日 17日 22日 28日 です。
|
2015年 六曜カレンダー/月齢カレンダー
|
六曜(六輝)は、吉凶を定める基準となる六つの日(先勝・友引・先負・仏滅・大安・赤口)の6種の日のことを指します
六曜は、日本で最も影響力のある暦注(れきちゅう)として、カレンダーや手帳などに幅広く記載され、結婚式には大安を選んだり、葬式には友引を避けたり、とくに冠婚葬祭などのセレモニーと深く結びついています。
|
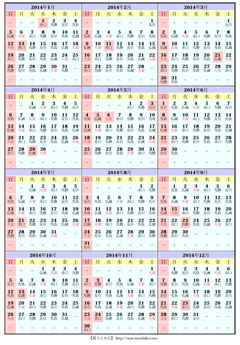
2015年 お日柄六曜カレンダー
|
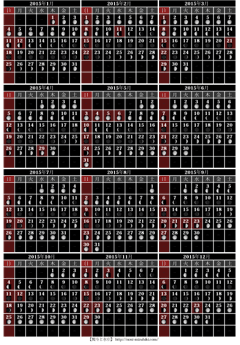
2015年 月齢カレンダー
|
現在では暦のお日柄と言えば、ほぼ間違いなくこの六曜のことをさしていると言ってよいでしょう。
単なる迷信とはいえ、慶事の贈答品などは、お日柄の良い日を選んだり、子どもの節句には、お日柄の良い日を選んで雛人形や五月人形を飾ったりするのが習慣となっています。
六曜について、さらに詳しく知りたい方は六曜と吉凶をご覧下さい。
過去も未来も、あらゆる年のカレンダーがダウンロードできる万年カレンダーは
こちらからどうぞ。
|
|
|
|